مدارهای خطی و خاصیت superposition
مقدمه
ما در دوره تحلیل مدار مقدماتی تاکنون برای تحلیل مدارهای خود از قوانین KVL و KCL و تحلیل گره ها استفاده کردیم. در این جلسه و چند جلسه آینده قصد داریم با یک سری از روش های متداول و بسیار مهم دیگر نیز آشنا شویم. این جلسه را به بررسی مفهوم مدارهای خطی و خواص آنها اختصاص داده ایم. مثل همیشه پیشنهاد می شود قبل از مطالعه این جلسه ابتدا جلسات زیر را مطالعه کنید:
معرفی مفهوم مدارهای خطی
مدار شکل زیر را ببینید:
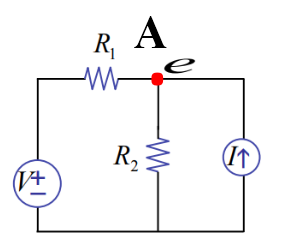
میخواهیم در این مدار ولتاژ گره A را بدست آوریم و قصد داریم از تحلیل گره استفاده کنیم. واضح است که به کمک تحلیل گره ، میتوانیم معادله زیر را بنویسیم :
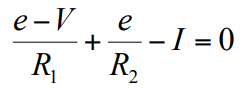
حال اگر کمی ساده سازی انجام دهیم و ولتاژ گره e را بدست آوریم ، به فرمی مشابه شکل زیر می رسیم :
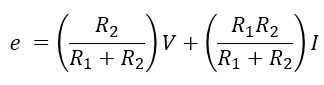
واضح است که ولتاژ گره e بر حسب منابع ولتاژ و جریان V و I یک رابطه خطی است. در واقع ما در این رابطه هیچ پارامتر غیر خطی نداریم. مثلا V به توان 2 یا VI یا هر نوع عبارتی که این رابطه را به یک رابطه غیر خطی تبدیل کند ، وجود ندارد. به عبارت ساده تر فرم این معادله ، یک معادله خطی است.
بررسی خواص مدارهای خطی
خاصیت خطی بودن ، یک خاصیت بسیار قوی است. و به ما کمک بسیار زیادی می کند تا این گونه مدارها را راحتتر تحلیل کنیم. این خاصیت دو ویژگی زیر را برای مدار در اختیار ما قرار می دهد. در واقع مدارهای خطی دو ویژگی زیر را دارند:
1- همگن بودن
2 -خاصیت superposition
حال بیایید و کمی در مورد این خواص صحبت کنیم. ابتدا با خاصیت همگن شروع می کنیم :
شکل زیر را ببینید :
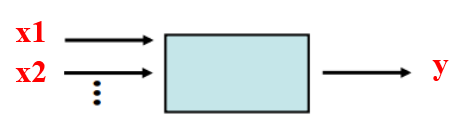
در این شکل ما تعدادی ورودی داریم که آنها را با x1 و x2 و … نشان داده ایم و یک خروجی هم با نام y داریم. اگر این سیستم همگن باشد در این اگر یک سیب سبز به ورودی آن بدهیم احتمالا خروجی آن یک سیب زرد خواهد بود.یعنی :
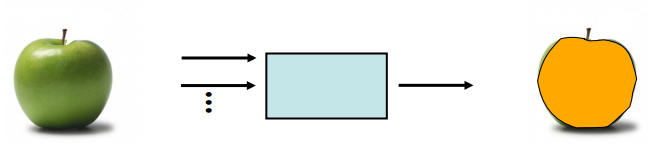
یعنی سیستم همگن ویژگی های ذاتی را حفظ کرده است و صرفا یک سری ویژگی های ظاهری مثل رنگ را عوض کرده است و در واقع ذات ورودی یعنی سیب بودن را تغییر نداده است. یعنی سیب را به یک انار تبدیل نکرده است. حال سیستم زیر را در نظر بگیرید:

در این شکل ورودی ها در یک alpha ضرب شده اند. ببینید اگر یک سیب گاز خورده در ورودی باشد ، خروجی به چه شکل خواهد بود :
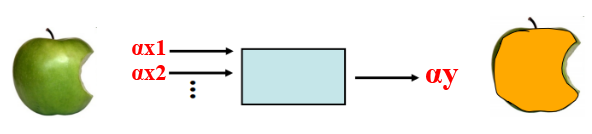
همانطور که میبینید، همچنان یک سیب در خروجی داریم که همچنان گاز خورده است و رنگش نیز تغییر کرده است و این بار اندازه اش نیز بزرگتر شده است.
حال به سراغ خاصیت دوم میرویم که بسیار کلیدی و مهم است.
معرفی خاصیت superposition
فرض کنید دو سیستم مشابه را داریم که به آنها ورودی های مختلفی اعمال می کنیم و خروجی های متناسب با ورودی نیز دریافت میکنیم. یعنی :
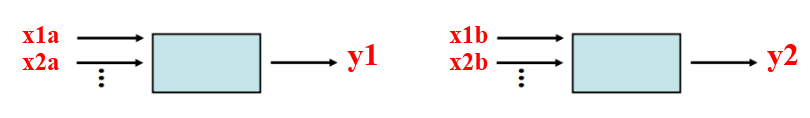
همانوطور که مشاهده میکنید برای سیستم شماره 1 ، x1a و x2a را به عنوان ورودی داده ایم و خروجی ya را دریافت کرده ایم و برای سیستم شماره 2 ، x1b و x2b را به عنوان ورودی داده ایم و خروجی yb را دریافت کرده ایم.
اگر بخواهیم با همان زبان سیب خودمان صحبت کنیم میتوانیم بگوییم که اگر به سیستم اول تعدادی سیب به ورودی بدهیم ، تعدادی از همان سیب را دریافت خواهیم کرد و اگر به سیستم دوم تعدادی موز بدهیم ، تعدادی موز نیز در خروجی دریافت خواهیم کرد.
حال بیایید یک کار انجام دهیم. سیستمی به نام سیستم شماره 3 در نظر بگیریم و ورودی های متناظر سیستم شماره 1 و سیستم شماره 2 را به عنوان ورودی به سیستم شماره 3 بدهیم. در واقع ورودی های متناظر را با هم جمع کنیم و به سیستم شماره 3 بدهیم. شکلی شبیه به شکل زیر میتواند این سیستم را توصیف کند :

همانطور که میبینید ، خروجی جمعی از خروجی تک تک ورودی ها شد. اگر بخواهیم با همان زبان سیبی صحبت کنیم هر ورودی سیستم شماره 3 شامل 1 سیب + 1 موز می باشد. خروجی نیز احتمالا یک سیب موز خوشمزه است !
پس به صورت خلاصه و مختصر متوانیم بگوییم :
اما این خاصیت چه کمکی به ما می کند ؟ بگذارید یک مثال برای این موضوع بزنیم.
مثال : فرض کنید سیستمی داریم که ورودی های V1 و V2 را داریم و میخواهیم خروجی این سیستم خطی را بدست آوریم. شکل زیر را ببینید:

دو راه برای این حل این مساله وجود دارد:
راه اول این است که به صورت مستقیم مساله را حل کنیم و ببینیم که اگر همه ورودی ها اعمال شوند ، نتیجه چه خواهد بود.
راه دوم این است که در ابتدا ورودی دوم را صفر کنیم و خروجی را بدست آوریم. در مرحله بعد ورودی اول را صفر کنیم و مجددا خروجی را بدست آوریم. سپس از superposition استفاده کنیم. یعنی:
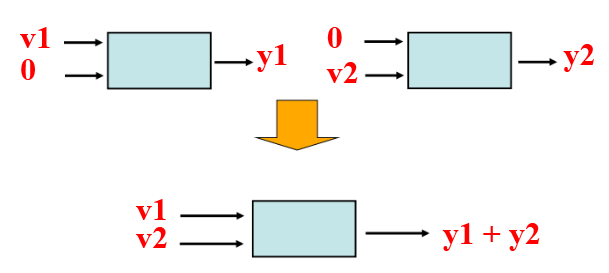
یعنی خروجی نهایی حاصل جمع تک تک خروجی هاست. در واقع وقتی ورودی های متناظر را با هم جمع کردیم ، خروجی های نیز با یکدگیر جمع می شوند.
اما این کار چه خاصیتی برای ما دارد و ما از این خاصیت در مدارهای خطی چگونه میتوانیم استفاده کنیم؟ به این سوال در جلسه بعد پاسخ خواهیم داد و مثالی را در این رابطه حل خواهیم کرد و البته یک آزمایش ساده و البته جالب در مورد مدارهای خطی نیز انجام خواهیم داد تا این موضوع را به خوبی درک کنیم.
سوال : مدار شکل زیر که از دو منبع ولتاژ و سه مقاومت تشکیل شده است را در نظر بگیرید: (مقادیر V1 و V2 و R1 و R2 و R3 را می دانیم.) جریان های i1 و i2 و ولتاژ v3 را میتوان به صورت ترکیبی خطی از V1 و V2 به صورت زیر نوشت : حال به کمک تحلیل گره هر یک از پارامترهای b1 , b2 , c1 , c2 , a2 , b1 را بر حسب مقاومت های R1 و R2 و R3 بدست آورید. 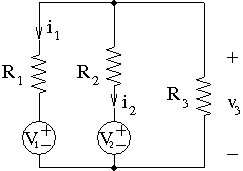
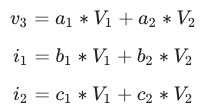
مثل همیشه میتوانید ما را در تلگرام و یا اینستاگرام دنبال کنید :




دیدگاهتان را بنویسید