آموزش numpy – بخش چهارم { آرایه ها و اندیس گذاری در numpy }

مقدمه

در جلسه چهارم از آموزش Numpy قصد داریم کار با آرایه های سه بعدی را با یکدیگر یاد بگیریم و علاوه بر آن با مبحث اندیس گذاری آشنا شویم و برخی از توابع آن را با یکدگیر مرور کنیم. پیشنهاد می شود حتما برای درک بهتر این جلسه ، جلسات قبلی این کتابخانه را از لینک زیر مطالعه کنید: 

• آموزش Numpy بخش اول (مقدمه و مرور کلی)
• آموزش Numpy بخش دوم (کار با ماتریس ها)
• آموزش Numpy بخش سوم (انجام محاسبات جبری)

ایجاد آرایه های سه بعدی به کمک Numpy

با آرایه های Numpy علاوه بر آرایه های یک بعدی و دو بعدی میتوانیم آرایه های سه بعدی نیز ایجاد کنیم. ایجاد این آرای به سادگی و با همان دستور np.array انجام می شود. در زیر یک آرایه سه بعدی ایجاد شده است : 

X = np.array( [[[  1, 2,3],              
                [ 4, 5, 6]],
               [[7,8,9],
                [10,11,12]]])

برای درک بهتر یک آرایه سه بعدی میتوانید این طور در نظر بگیریم که در ابتدا آرایه دو بعدی [[4,5,6],[1,2,3]] وجود دارید که در لایه بالایی قرار دارد و سپس یک آرایه دو بعدی دیگر که [[10,11,12],[7,8,9]]  می باشد در زیر آن قرار گرفته است. در واقع انگار یک ماتریس داریم که عمق دارد. چیزی شبیه به شکل زیر : 

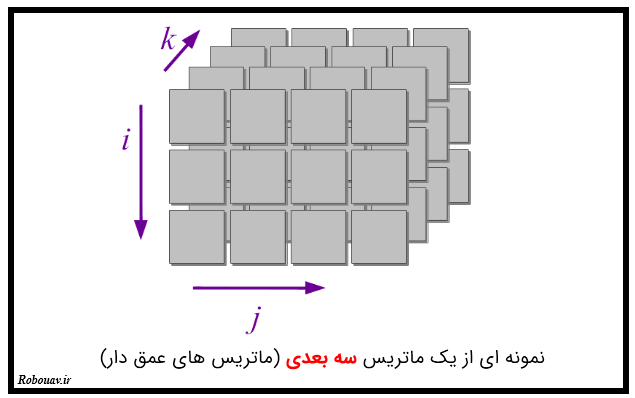
شاید بپرسید که آرایه های سه بعدی در کجا کاربرد دارند. ساده ترین و البته یکی از مهمترین کاربردهای آرایه های سه بعدی در تصاویر رنگی است. قابل ذکر است که کتابخانه ای مثل OpenCV در نسخه پایتون خود برای نمایش تصاویر از همین کتابخانه Numpy استفاده می کند. 

برای دیدن شکل آرایه ، تعداد ابعاد و تعداد المان ها میتوانید از متد های shape و ndim و size استفاده کنید. مثلا اگر میخواهید شکل آرایه X که در بالا تعریف شد را بیابید کافی است تا دستور X.shape را در ویرایشگر خود وارد کنید. (سعی کنید این کار را برای متدهای ndim و size انجام دهید.) 

اگر بخواهیم به عنوان مثال یک عملیات ریاضی مثل جمع را صرفا برای یکی از این سه بعد انجام دهیم ، کافی است تا از آرگومان axis که نشان دهنده ی بعد می باشد استفاده کنیم. در مثال زیر جمع المان ها برای روی هر یک از سه بعد انجام شده است : 

X.sum(axis = 0)
X.sum(axis = 1)
X.sum(axis = 2)

تذکر : قبل از این که این کدها را اجرا کنید ، فکر کنید و حدس بزنید که نتیجه به چه شکل خواهد بود. 

با اجرای کد بالا نتیجه به صورت زیر می باشد: 

X.sum(axis = 0)
Output: 
array([[ 8, 10, 12],
       [14, 16, 18]])

X.sum(axis = 1)
Output: 
array([[ 5,  7,  9],
       [17, 19, 21]])

X.sum(axis = 2)
Output: 
array([[ 6, 15],
       [24, 33]])

بیایید نتایج بالا را کمی دقیق تر تحلیل کنیم. 

ابتدا آمده ایم و مجموع المان های بعد شماره صفر را محاسبه کرده ایم. این بعد همان عمق ماتریس ما می باشد. در واقع المان های ماتریس تک به تک در راستای محور z با یکدگیر جمع می شوند و نتیجه در خروجی نشان داده می شود. 

در گام بعد مجموع المان ها در راستای محور y ها محاسبه شده است. همانطور که گفتیم این ماتریس از دو ماتریس دو بعدی تشکیل شده است که بر روی یکدیگر قرار گرفته اند. حال در این مرحله برای هر کدام از این ماتریس ها ، المان های آن به صورت عمودی با یکدگیر جمع می شوند و به عنوان یک المان از ماتریس جدید در نظر گرفته می شود. یعنی برای ماتریس بالایی 1و 4 با یکدگیر جمع می شوند و به عنوان عدد 5 در ماتریس نهایی قرار داده می شود. این کار برای اعداد 2 و 5 و سپس 3 و 6 نیز انجام می شود. 

پس از این که محاسبات برای ماتریس بالایی انجام شد حالا نوبت انجام همین محاسبات برای ماتریس پایینی نیز می رسد و همین کارها برای آن ماتریس انجام می شود و نتیجه در یک ردیف جدید از ماتریس نهایی قرار داده می شود و نتیجه خروجی که یک ماتریس دو بعدی است حاصل می شود. 

در انتها نیز باید محاسبات را برای محور x که با پارامتر axis=2 مشخص می شود ، انجام دهیم. مطابق توضیحات مرحله قبل برای ماتریس بالایی ابتدا المان های 1و 2و 3 با یکدگیر جمع می شوند و نتیجه در ماتریس نهایی قرار داده می شود. سپس این کار برای ماتریس پایینی نیز انجام می شود و ماتریس نهایی بدست آورده می شود. 

نوشتن ماتریس سه بعدی به صورت یک ماتریس تک بعدی : 

اگر بخواهیم ماتریس سه بعدی X را به صورت یک ماتریس تک بعدی بنویسیم که همه المان های ان در ردیف قرار گرفته اند ، میتوانیم از دستور ravel استفاده کنیم. مثال زیر را ببینید :

X.ravel()

با اجرای کد بالا نتیجه به صورت زیر خواهد بود :

 array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

اندیس گذاری در آرایه ها

مهمترین نکته مبحث اندیس گذاری این است که در پایتون اندیس ها از 0 شروع می شوند. بقیه مباحث مربوط به اندیس گذاری بسیار ساده است. 
به صورت کلی اگر بخواهیم یک فرمول کلی برای مباحث مربوط به اندیس ارایه کنیم میتوانیم شکل زیر را در نظر بگیریم : 

حال با توجه به شکل بالا مثلا اگر بخواهیم المان دوم از یک آرایه تک بعدی را استخراج کنیم کافی است از [X[3 استفاده کنیم. علاوه برآن اگر بخواهیم المان های 4 تا 9 یک آرایه تک بعدی را استخراج کنیم کافی است تا از [X[4:10 استفاده کنیم. قطعا یک مثال برای درک بهتر این موضوع به ما کمک بیشتری می کند : 

x = np.arange(10)
x[2]
x[2:5]

همانطور که میبینید در ابتدا به کمک تابع arange (که قبلا آن را توضیح داده ایم ) یک آرایه تک بعدی از 0 تا 9 تشکیل داده ایم. سپس در خط دوم المان سوم این آرایه را خواسته ایم. در انتها نیز در خط سوم المان های 2 و 4 آرایه را استخراج کرده ایم. 

با اجرای قطعه کد بالا نتیجه به صورت زیر خواهد بود :

 x[2]
Output: 2

x[2:5]
Output: array([2, 3, 4])

حال فرض کنید که میخواهیم المان های این آرایه را تغییر دهیم. 

به عنوان مثال قصد داریم المان هایی که از اول شروع می شوند تا سر المان 7 ام (خود 7 را شامل نمی شود) با گام های 3 تایی تغییر دهیم (یعنی اولی را که تغییر دادیم سه تا برویم جلو و سپس بعدی را تغییر دهیم.) . این کار را بر روی آرایه x که در بالا تعریف شده است ، انجام می دهیم. 

تذکر : سعی کنید قبل از خواندن ادامه این متن ابتدا خودتان به این موضوع فکر کنید و کد مربوط به این قسمت را بنویسید و سپس ادامه این متن را بخوانید. 

برای این کار میتوانیم از کد مشابه با زیر استفاده کنیم. 

x[:7:3] = 123

واضحی است که در ابتدا برای این که المان ها را از اول شروع کنیم برای قسمت اول هیچ مقداری قرار ندادیم. برای این که محل پایان را مشخص کنیم عدد 7 را قرار داده ایم تا نشان دهیم که میخواهیم تغییرات حداکثر تا جایگاه هفتم انجام شود. در بخش سوم نیز اندازه گام ها را مشخص کنیم که واضح است در اینجا اندازه گام ها برابر با 3 می باشد. 

حال اگر در خروجی x را بنویسیم و بخواهیم که مقدار آن به ما نمایش داده شود ، در این صورت x چنین خواهد بود : 

 array([123,   1,   2, 123,   4,   5, 123,   7,   8,   9])

در پایان جلسه برای درک بهتر پیشنهاد می شود حتما تمارین زیر را انجام دهید : 

مثل همیشه در پایان میتوانید ما را در تلگرام و یا اینستاگرام دنبال کنید :