آموزش Numpy – بخش سوم {انجام محاسبات جبری}

مقدمه

در جلسه اول و دوم آموزش Numpy به معرفی این ماژول و کار با آرایه های یک بعدی و دو بعدی پرداختیم. در این جلسه قصد داریم انجام محاسبات جبری با ماتریس ها را به کمک این ماژول انجام دهیم. قبل از ورود به بحث اصلی پیشنهاد می شود برای فهم بهتر این مطلب حتما جلسات اول و دوم این آموزش را از لینک های زیر مطالعه کنید : 

• آشنایی با Numpy و توابع آن 
• ایجاد و کار با آرایه های یک بعدی و دو بعدی با Numpy

نکته : دوستان عزیز ، خواندن این جلسه به تنهایی کافی نمی باشد و یادگیری عمیقی برای شما ایجاد نخواهد کرد. لطفا یک ادیتور باز کنید و تمامی کدهایی که در ادامه جلسه آورده می شوند را خودتان امتحان کنید و گام به گام با آموزش پیش بروید تا تمامی این آموزش ها را یک بار برای همیشه یاد بگیرید. 

محاسبات جبری با ماتریس ها

اجازه بدهید قبل از این که به انجام محاسبات جبری با ماتریس ها بپردازیم ، ماتریس های مورد نیاز خود را که درادامه با آنها کار خواهیم کرد را ایجاد کنیم. به کمک دستورات زیر این کار را میتوانیم انجام دهیم  :

A = np.array([[2,0,1],[4,3,8],[7,6,9]])
b = np.array([1,101,14])
B = np.array([[10,20,30],[40,50,60],[70,80,90]])

حال  سه متد مهم برای کار با ماتریس ها معرفی میکنیم : 

• متد A.transpose  : به کمک این متد میتوانیم Transpose یک ماتریس را بدست آوریم. 
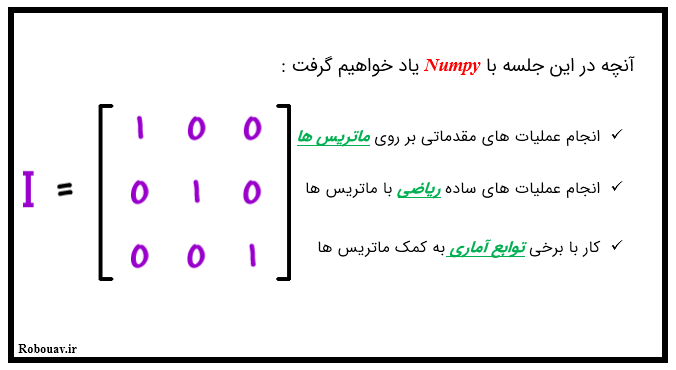
• متد np.trace : با این متد میتوان trace یک ماتریس را بدست آورد. (trace در واقع مجموعه درایه های قطر اصلی ماتریس می باشد.)
• متد np.linalg.inv : با این متد میتوان معکوس یک ماتریس را محاسبه کرد. 

در زیر مثال های مربوط به این سه متد آورده شده است : 

A.T             #transpose
A.transpose()  #transpose
np.trace(A)  # trace
np.linalg.inv(A)  #Inverse

همانطور که مشاهده میکنیم به جای متد transpose میتوانیم از T هم استفاده کنیم. 

در نهایت و با اجرای کدهای بالا ، نتیجه خروجی به صورت زیر حاصل می شود : 

A.transpose()  #transpose
Output: 
array([[2, 4, 7],
       [0, 3, 6],
       [1, 8, 9]])

np.trace(A)  # trace
Output: 14

np.linalg.inv(A)  #Inverse
Output: 
array([[ 0.53846154, -0.15384615,  0.07692308],
       [-0.51282051, -0.28205128,  0.30769231],
       [-0.07692308,  0.30769231, -0.15384615]])

توجه داشته باشید که متد transpose آرایه اصلی را تغییر نمی دهد. 

جمع و تفریق ماتریس ها : به سادگی و به کمک علامت های جمع و تفریق میتوانیم ، جمع و تفریق ماتریس ها را انجام دهیم : 

A+B
A-B

مثال زیر را ببییند : 

A+B
Output: 
array([[12, 20, 31],
       [44, 53, 68],
       [77, 86, 99]])

A-B
Output: 
array([[ -8, -20, -29],
       [-36, -47, -52],
       [-63, -74, -81]])

 ضرب ماتریس ها : برای ضرب دو ماتریس با numpy کافی است از متد dot استفاده کنیم. در واقع اگر بخواهیم مثلا ضرب ماتریسی A.B را انجام دهیم در این صورت کافی است از عبارت (A.dot(B  استفاده کنیم. مثال زیر را ببینید: 

A.dot(B)

با اجرای کد بالا نتیجه به صورت زیر حاصل می شود : 

array([[  90,  120,  150],
       [ 720,  870, 1020],
       [ 940, 1160, 1380]])

 حل یک معادله خطی : برای حل معادله خطی Ax=b که در آن x مجهول می باشد از دستور np.lilang.solve استفاده میکنیم. مثال زیر را ببییند: 

np.linalg.solve(A,b)

با اجرای کد بالا نتیجه به صورت زیر خواهد بود : 

array([-13.92307692, -24.69230769,  28.84615385])

 محاسبه مقدار ویژه و بردار ویژه ماتریس ها : برای محاسبه مقدار ویژه و بردار ویژه یک ماتریس کافی است از دستور np.linlang.eig استفاده کنیم. مثلا : 

np.linalg.eig(A)

که نتیجه خروجی اجرای این دستور به صورت زیر است : 

(array([ 14.0874236 ,   1.62072127,  -1.70814487]),
 array([[-0.06599631, -0.78226966, -0.14996331],
        [-0.59939873,  0.54774477, -0.81748379],
        [-0.7977253 ,  0.29669824,  0.55608566]]))

ردیف اول جواب خروجی مقدار ویژه های این ماتریس است  و ماتریس بعدی هم ماتریس بردار ویژه ها است به صورتی که هر ستون ماتریس متناظر با مقدار ویژه محاسبه شده در ردیف اول می باشد. 

کار با برخی توابع پایه ریاضی

با numpy و به سادگی هر چه تمام تر میتوانیم از توابع مثلثاتی مثل sin و cos و … استفاده کنیم. مثال زیر گویایی همه چیز است : 

B = np.array([[0,-20,36],[40,50,1]])
np.sin(B)

که نتیجه اجرای خروجی به صورت زیر می باشد : 

array([[ 0.        , -0.91294525, -0.99177885],
       [ 0.74511316, -0.26237485,  0.84147098]])

ماتریس خروجی در واقع سینویس تک تک المان های ماتریس ورودی را محاسبه می کند. توجه کنید که این متد هر کدام از المان های ورودی را بر حسب رادیان در نظر میگیرد و سپس سینوس آن را محاسبه می کند. 

 به توان رساندن المان های ماتریس ها : برای این که توان های المان های یک ماتریس را محاسبه کنیم کافی از عملگر ** استفاده کنیم. مثلا فرض کنیم میخواهیم المان های ماتریس B را به توان 2 برسانیم. در این صورت میتوانیم بنویسیم : 

B**2

و با اجرا کد بالا خواهیم داشت : 

array([[   0,  400, 1296],
       [1600, 2500,    1]], dtype=int32)

و در واقع به سادگی المان های ماتریس B هر کدام به توان 2 رسیده اند. 

بدست آوردن ریشه و مقدار مطلق و نمایی یک ماتریس : 

• محاسبه ریشه تک تک المان ها : برای این کار از دستور np.exp استفاده میکنیم. 
• محاسبه قدر مطلق تک تک المان ها : برای این کار از دستور np.absolute استفاده میکنیم. 
• محاسبه مقدار نمایی هر المان : منظور از مقدار نمایی هر المان این است که آن المان به توان عدد نپر (e) برسد. برای این کار نیز کافی است از متد np.exp استفاده کنیم.

مثال زیر را ببینید : 

np.absolute(B)
np.sqrt(B)
np.exp(B)

انجام برخی از عملیات های آماری بر روی ماتریس ها

ابتدا ماتریس A را به صورت زیر در نظر بگیرید : 

A = np.arange(1,10).reshape(3,3)
A

همانطور که میدانیم این ماتریس به صورت زیر می باشد: 

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

حال میخواهیم برای این مجموعه داده ها( که در قالب یک ماتریس هستند ) جمع ، مینیمم ، ماکزیمم ، میانگین ، انحراف از معیار و واریانس را محاسبه کنیم. دستورات زیر به ترتیب هر کدام از عملیات های زیر را انجام میدهد : 

A.sum()
A.min()
A.max()
A.mean()
A.std()   #Standard deviation
A.var()  #Variance

با اجرای کدهای بالا نتیجه زیر حاصل می گردد: 

A.sum()
Output: 45

A.min()
Output: 1

A.max()
Output: 9

A.mean()
Output: 5.0

A.std()   #Standard deviation
Output: 2.5819888974716112

A.var()
Output: 6.666666666666667

برای محاسبه اندیس بیشترین و یا کمترین المان کافی است از متدهای argmin و argmax استفاده کنیم :

A.argmin()
A.argmax()

نتیجه اجرای کد بالا به صورت زیر می باشد: 

A.argmin()
Output: 0

A.argmax()
Output: 8

اگر بخواهیم هر کدام از این عملیات های آماری را بر روی یک ردیف یا ستون مشخص انجام دهیم کافی است پارامتر axis را تنظیم کنیم. برای یک ماتریس این پارامتر میتواند دو مقدار 0 و 1 را به خود بگیرد. وقتی که مقدار این پارامتر صفر می باشد منظور این است که عملیات بر روی ستون ها انجام می شود و وقتی مقدار این پارامتر 1 است منظور این است که عملیات های مورد نظر بر روی ردیف ها انجام می گردد. به مثال های زیر توجه کنید :

A.sum(axis=0)              
A.mean(axis = 0)
A.std(axis = 0)
A.argmin(axis = 0)

در مثال بالا همه عملیات های انجام شده بر روی ستون ها انجام می شود. مثلا به کمک عبارت اول جمع المان های تک تک ستون ها انجام می شود و نتیجه در خروجی نمایش داده می شود. با اجرای کد بالا نتیجه به صورت زیر خواهد بود : 

A.sum(axis=0)                 # sum of each column, it will move in downward direction
Output: array([12, 15, 18])

A.mean(axis = 0)
Output: array([ 4.,  5.,  6.])

A.std(axis = 0)
Output: array([ 2.44948974,  2.44948974,  2.44948974])

A.argmin(axis = 0)
Output: array([0, 0, 0], dtype=int64)

به عنوان مثال دیگر ، فرض کنید که میخواهیم مینیمم هر کدام از ردیف ها و اندیس ماکزیمم هر کدام از ردیف ها را محاسبه کنیم. در این صورت میتوان نوشت :

A.min(axis=1)
A.argmax(axis = 1)

که با اجرای کد بالا خواهیم داشت : 

A.min(axis=1)                  # min of each row, it will move in rightwise direction
Output: array([1, 4, 7])

A.argmax(axis = 1)
Output: array([2, 2, 2], dtype=int64)

به عنوان مثال آخر فرض کنید میخواهیم جمع انباره ای هر یک از ردیف ها را پیدا کنیم. در واقع میخواهیم برای هر ردیف هر المان را با مجموع المان های قبلی جمع کنیم. برای این کار کافی است از دستور cumsum استفاده کنیم و چون میخواهیم این کار را برای ردیف ها انجام دهیم ، پس مقدار پارامتر axis را بر روی 1 تنظیم میکنیم و بنابراین : 

A.cumsum(axis=1)

و نتیجه خروجی نیز به صورت زیر می باشد: 

array([[ 1,  3,  6],
       [ 4,  9, 15],
       [ 7, 15, 24]], dtype=int32)

در پایان جلسه برای درک بهتر این جلسه پیشنهاد می شود تمرین های زیر را انجام دهید : 

این جلسه هم به پایان رسید. مثل همیشه میتوانید ما را در تلگرام و یا اینستاگرام دنبال کنید :