معادله دیفرانسیل مرتبه اول – { جلسه اول دوره تحلیل مدار مقدماتی }

مقدمه

در اولین جلسه از دوره آموزش تحلیل مدار ، طبق سرفصل ها باید مروری بر معادلات دیفرانسیل داشته باشیم. در این جلسه معادله دیفرانسیل مرتبه اول و نحوه حل آنها را با یکدگیر مرور میکنیم. توجه کنید که این جلسه صرفا یک مرور می باشد و ما به صورت کلی با این معادلات و روش حل آنها آشنا می شویم و برای جزییات بیشتر حتما لازم است تا کتاب های مرجع مطالعه شوند. 

دوست عزیز ، خواندن این جلسه بدون انجام تمرینات آن و گام به گام پیش رفتن با درس تاثیر چندانی ندارد. لطفا همین الان یک قلم و کاغذ بردارید و گام به گام با محاسبات و مراحل این جلسه پیش بروید تا خودتان به درک عمیقی از این مطالب برسید و یک بار برای همیشه بتوانید الکترونیک را خوب یاد بگیرید و مدارها را دقیق تحلیل کنید.

معرفی معادله دیفرانسیل مرتبه اول

قبل از هر چیز بهتر است بدانیم که دقیقا چه نوعی از معادله دیفرانسیل مرتبه اول را میخواهیم مورد بررسی قرار دهیم. اگر به کتابهای مرجع مراجعه کنید ، احتمالا معادل انگلیسی معادلاتی که امروز بررسی می شوند ، چیزی شبیه به اصطلاح زیر می باشد: 

“Linear firest Order Constant Coefficient DEs”

که یعنی قصد داریم معادلاتی به فرم زیر را بررسی کنیم : 

اما منظور از آن چیست ؟ 

در معادله بالا A  و B ضرایبی ثابت هستند. به همین خاطر در عبارت انگلیسی بالا از “Constant Coefficient ” آورده شده است که به معنی ضرایب ثابت می باشد. علاوه بر آن بیشترین درجه مشتق هم 1 می باشد. به همین علت از first Order استفاده کرده ایم. عبارت DE هم یعنی Differential Equations که به معنای معادلات دیفرانسیل می باشد. پس به صورت خلاصه میتوانیم عبارت انگلیسی بالا را به صورت زیر ترجمه کنیم : 

“معادله دیفرانسیل مرتبه اول خطی با ضرایب ثابت “

حال میخواهیم پاسخ این معادلات را بدست آوریم. 

بدست آوردن پاسخ معادلات دیفرانسیلی خطی مرتبه اول با ضرایب ثابت : 

از درس معادلات دیفرانسیل به یاد داریم که میتوانیم برای این معادله دو پاسخ خصوصی و همگن را بدست آوریم. اما این دو پاسخ به چه معنایی می باشند: 

پاسخ خصوصی (xp) : برای محاسبه xp کافی است یک حدس اولیه از جواب معادله بزنیم و سپس با قرار دادن حدس اولیه در معادله اصلی ضرایب حدس خود را بدست آوریم. در ادامه در مورد این موضوع بیشتر صحبت می کنیم.

پاسخ همگن (xh): برای محاسبه پاسخ همگن کافی است سمت راست معادله را مساوی صفر قرار دهیم و جواب را بدست آوریم. 

پاسخ نهایی : پاسخ نهایی یک معادله دیفرانسیلبرابر با x = xh + xp می باشد. به سادگی و با قرار دادن این جواب در معادله اصلی میتوانیم این موضوع را اثبات کنیم. اما برای کوتاه تر شدن مطلب از انجام آن خودداری میکنیم. (خودتان برای تمرین بیشتر حتما این کار را انجام دهید.)

مقدمه

حال با توجه به توضیحات بالا یک مثال میزنیم و تمامی موارد بالا را از روی آن مثال بدست می آوریم. 

فرض کنید که معادله زیر را میخواهیم حل کنیم : 

همانطور که در بالا گفته شد باید دو پاسخ خصوصی و همگن برای این معادله را بدست آوریم. ابتدا پاسخ همگن را محاسبه می کنیم : 

محاسبه پاسخ همگن : همانگونه که در بالا توضیح داده شده ، برای بدست آوردن پاسخ همگن باید طرف راست معادله را صفر کنیم. یعنی معادله زیر را حل کنیم : 

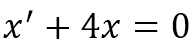
معادله بالا را میتوانیم به صورت زیر بنویسیم : 

بدست آوردن پاسخ این معادله کار سختی نیست و اثبات ریاضی کوتاهی دارد ولی به عنوان یک نکته به یاد داشته باشید که اگر معادله ای به فرم زیر داشته باشیم : 

حل آن به صورت زیر خواهد بود: 

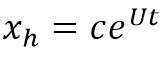
که در آن c یک ضریب ثابت است. توجه داشته باشید که در تمامی معادلات بالا x بر حسب t می باشد و نتیجه نهایی نیز باید بر حسب t (که یک پارامتر است ) باشد. حتما پاسخ بالا در معادله قرار دهید و از صحیح بودن آن اطمینان حاصل کنید. 

با تفاسیر بالا پاسخ همگن معادله ما به صورت زیر می باشد: 

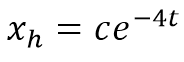
حال باید پاسخ خصوصی را محاسبه کنیم تا بتوانیم پاسخ معادله را بدست آوریم. 

محاسبه پاسخ خصوصی : پاسخ خصوصی بر پایه یک حدس می باشد. البته این حدس برای فرم های خاصی از معادلات دیفرانسیل از قبل زده شده است و ما نیز از همان حدس ها استفاده می کنیم. 

حدسی که برای این معادلات زده می شود به صورت x = N است که N یک عدد ثابت می باشد و باید با جایگذاری در معادله آن را محاسبه کنیم. بنابراین خواهیم داشت : 

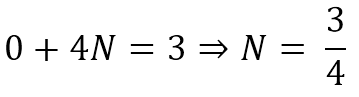
در بالا ما تنها N را در معادله اصلی خود جایگذاری کرده ایم. توجه کنید که چون N یک عدد ثابت است ، پس مشتق اول آن نیز صفر می باشد و به همین دلیل ترم اول معادله صفر شده است. 

پس پاسخ خصوصی نیز به صورت xp = 3/4 می باشد. حال میتوانیم پاسخ کامل را محاسبه کنیم : 

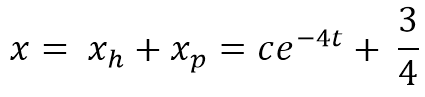
توجه کنید که c در اینجا میتواند هر عددی باشد و به ازای تمامی اعداد پاسخ معادله است. 

در این جلسه ما معادله دیفرانسیل مرتبه اول را با یکدگیر مرور کردیم. قبل از پایان این جلسه تمریناتی آورده شده است که پیشنهاد جدی ما انجام آن است. بدون انجام آن یادگیری شما کامل نمی شود. 

در پایان مثل همیشه میتوانید ما را در تلگرام و یا اینستاگرام دنبال کنید: