معادلات سینماتیک حاکم بر کوادروتور با استفاده از معادلات اویلر{جلسه دوم}

مقدمه

قبل از شروع به خواندن مطالب این جلسه از لینک زیر جلسه قبل را مطالعه نمایید.

طراحی یک کنترل کننده برای کوادروتور{جلسه اول}

کوادروتور

کوادروتور دارای شش درجه آزادی می باشد به همین دلیل قابلیت انجام مانورهای پیچیده را دارا می باشد و با تغییر سرعت ملخ ها می توان انواع حرکات آکروباتیک را انجام داد. همانطور که در شکل زیر نیز مشاهده می کنید هر روتور با چرخش خود باعث ایجاد نیروی لیفت و گشتاور در هر گوشه از کوادروتور می شود که با تغییر نیروی لیفت و گشتاور  به وسیله سرعت روتورها حرکت این وسیله انجام میشود. هر گونه تغییر کوچکی در نیروی تراست یکی از موتورها باعث ناپایداری می شود و بایستی نیروی تراست هر موتور به دقت کنترل شود تا پایداری کوادروتور از بین نرود. کنترل دستی هر چهار موتور بسیار دشوار و حتی غیرممکن است بنابراین به منظور تامین یک پایداری مطمعن نیاز به طراحی یک اتوپایلوت است.

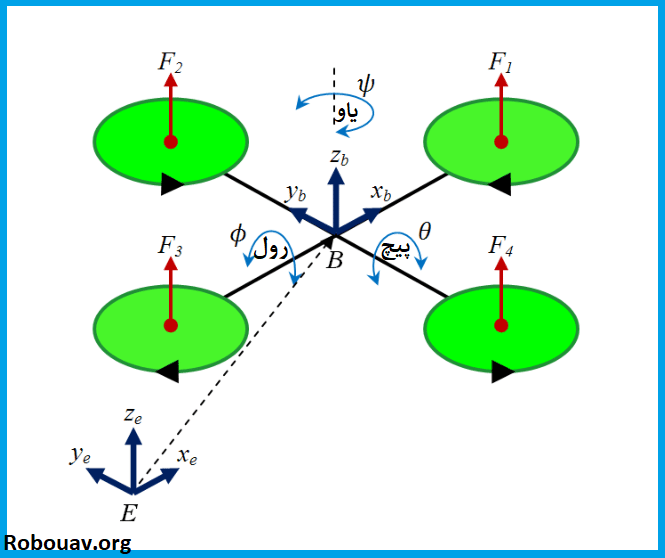در شکل زیر مشاهده می کنید که کوادروتور دارای 4 نوع مانور حرکتی می باشد. که به صورت زیر است:

1. رول
2. پیچ
3. یاو
4. تراتل

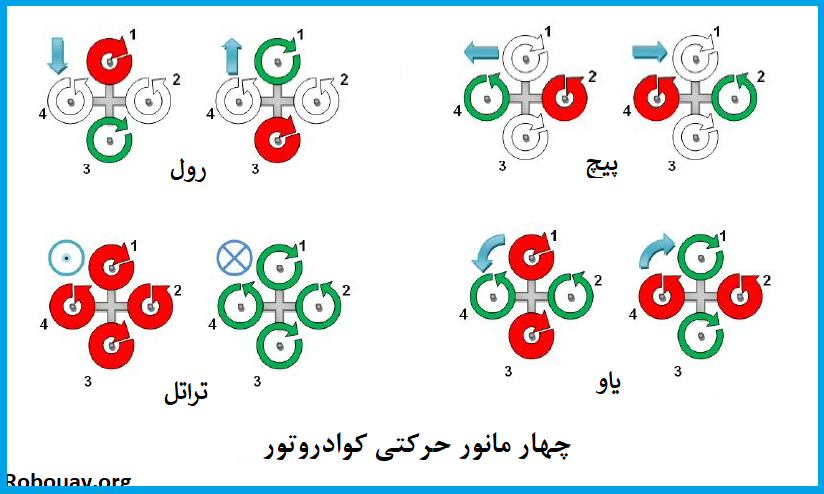
همانطور که قبلا گفتیم کوادروتور دارای 6 درجه آزادی است و از طرفی دارای 4 مانور حرکتی است. به سیستم های کنترلی که تعداد ورودی های کنترلی آنها کمتر از درجه آزادیشان می باشد سیستم های Underactuated گفته می شود.

معادلات اویلر

با استفاده از معادلات سینماتیک قصد داریم معادلات حاکم بر کوادروتور را تعیین کنیم. همانگونه که میدانید سینماتیک به مطالعه حرکت اجسام بدون در نظر گرفتن نیروها و گشتاورهای حاکم بر آن می پردازد. برای توصیف حرکت یک جسم صلب شش درجه آزادی دو فریم مرجع تعریف میکنیم:

1. مرجع اینرسی زمین(فریم E)
2. مرجع فیکس شده به جسم(فریم ‌B)

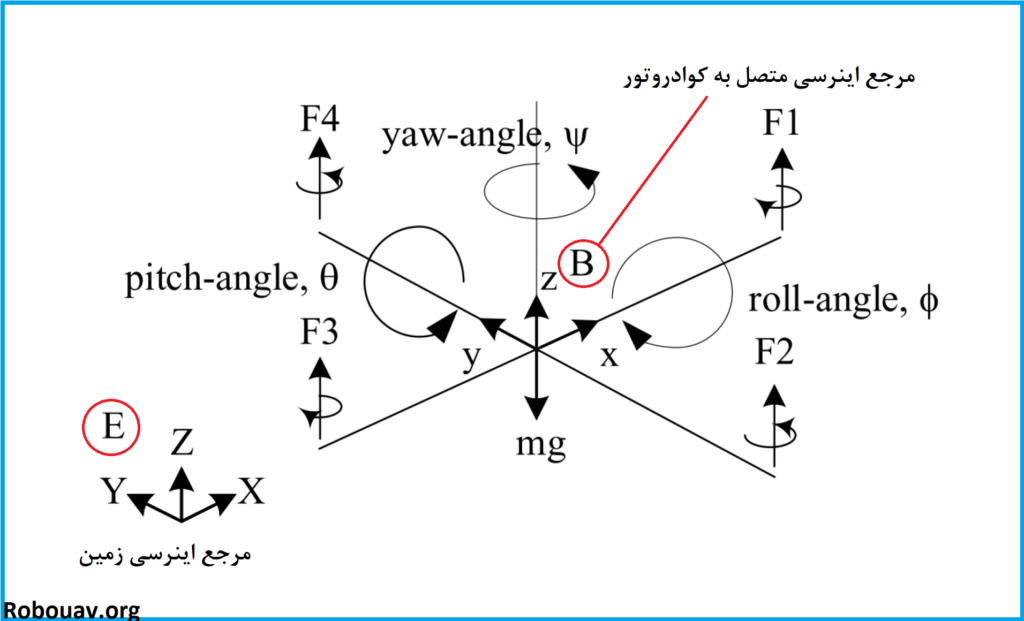
فریم E که دارای چهار مولفه  OE, XE, YE, ZE می باشد.

XE: در جهت شمال

YE: در جهت غرب

ZE: به سمت بالا

OE: مبدا فریم متصل به زمین

برای تعیین موقعیت خطی کوادروتور( Γ^E )به وسیله بردار بین فریم E و فریم B می توان استفاده کرد و با استفاده از سه پارامتر X , Y و Z می توان موقعیت خطی کوادروتور را پیدا کرد.

[X Y Z]=Γ^E 

تا اینجا موقعیت خطی فریم B نسبت به فریم E تعیین شد. حال برای دقیق تر مشخص شدن موقعیت فریم ها نسبت به هم لازم است که موقعیت زاویه ای فریم B نسبت به E نیز مشخص شود که برای این منظور از بردار زیر استفاده می کنیم:

^{_{[φ θ ψ]=θ}E}

ماتریس دوران R^_θ به وسیله ضرب سه ماتریس دوران پایه به دست می آید که به صورت تصویری در زیر نشان داده شده است:

دوران حول محور X:

دوران حول محور Y:

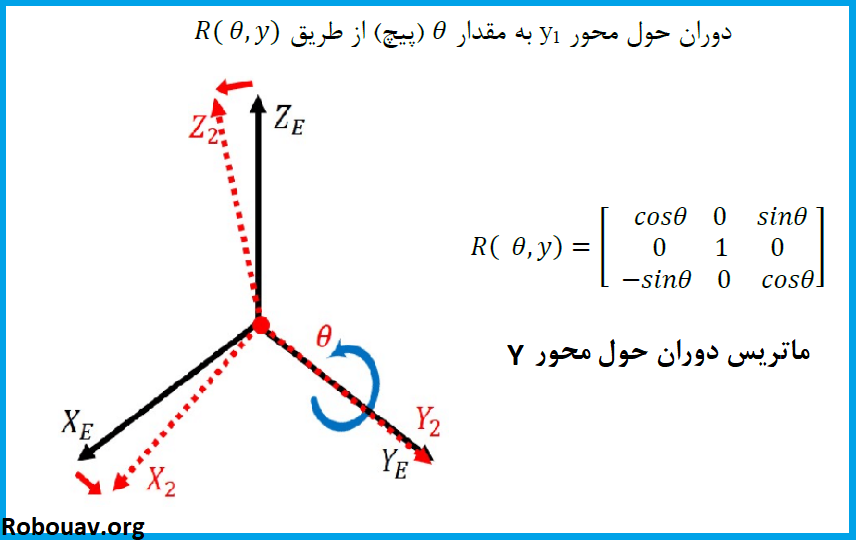
دوران حول محور Z:

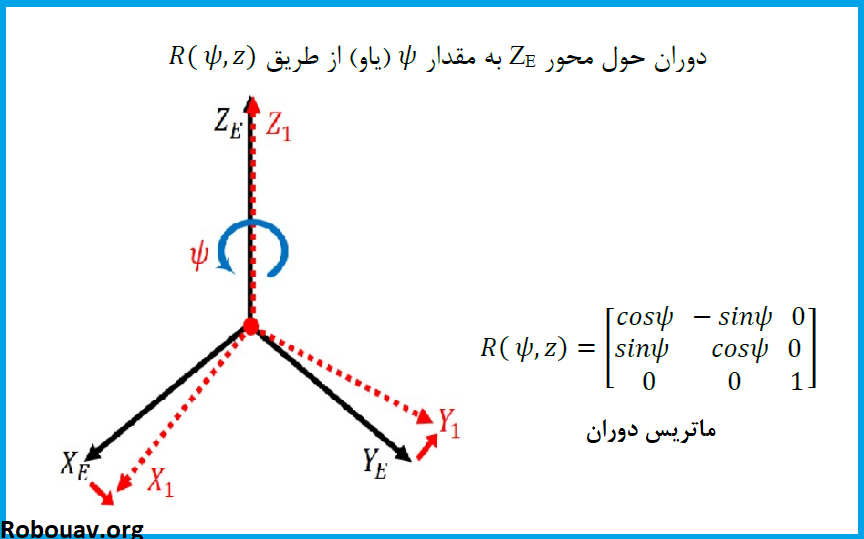
ماتریس دوران نیز از ضرب سه ماتریس اصلی چرخش حول محورها به دست می آید که به صورت زیر است:

در ماتریس دوران بالا پارامتر ستون اول و سطر اول را با R11 و سطر اول ستون دوم را با R12 و به همین ترتیب بقیه پارامترها را تعریف می کنیم.

برای به دست آوردن یک نمایش کامل از جسم در فضا می بایست کمیت های زاویه ای و خطی با هم ترکیب شوند بنابراین پارامترهای زیر را تعریف می کنیم:

ارتباط بین سرعت های خطی در فریم متصل به کوادروتور و فریم متصل به زمین را می توان به وسیله فرمول زیر محاسبه کرد:

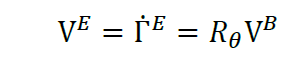
همچنین مشابه سرعت های خطی می توان سرعت های زاویه ای در دو فریم متصل به جسم(‌B) و فریم متصل به زمین(E) را با استفاده از ماتریس فرمول زیر و ماتریس انتقال T به دست آورد:

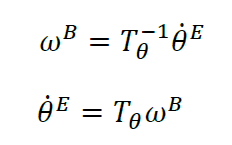
که در آن ماتریس انتقال T به وسیله بازحل معادلات اویلر به دست می آید:

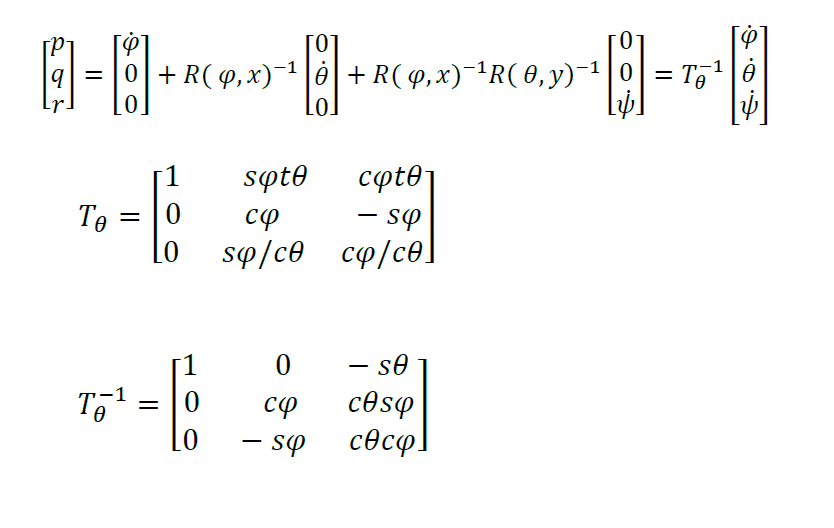
در ماتریس های بالا از علایم اختصاری استفاده شده است که به صورت زیر است:

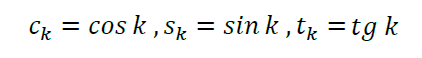
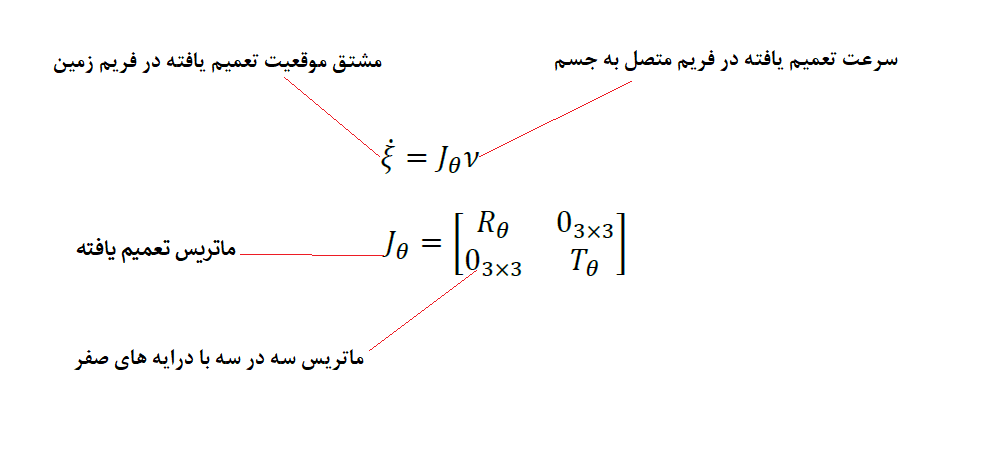
معادلات سرعت خطی و سرعت زاویه ای می توانند با هم ترکیب شوند و در یک معادله آورده شوند به طوری که مشتق موقعیت تعمیم یافته در فریم زمین را به سرعت تعمیم یافته در فریم متصل به جسم مرتبط کند. 

دوستان عزیز بیشتر دوره های مربوط به این وب سایت رایگان می باشد. در صورت تمایل می توانید به اندازه وسع مالی خود(هر چند ناچیز) جهت پرداخت هزینه های نگهداری وب سایت از ما حمایت کنید:

این جلسه هم به پایان رسید. برای اطلاع از جلساتی که در آینده بر روی سایت قرار داده می شود و همچنین مطالبی که در کانال ما منتشر می شود می توانید ما را در محیط های مجازی دنبال کنید:

کانال تلگرام ما

اینستاگرام ما