مروری بر قوانین کیرشهف {KVL و KCL}
مقدمه
در این جلسه قصد داریم به معرفی دو قانون مهم در برق و الکترونیک (که احتمالا همه ما حداقل یک بار با آنها برخورد داشته ایم) بپردازیم. به کمک این دو قانون میتوانیم مدارهایی را که در جلسه و جلسات آینده معرفی می کنیم ، تحلیل کنیم.
قانون KCL
قبل از معرفی قانون KCL بهتر است با مفهوم گره آشنا شویم :
تعریف گره : در مدارهای الکتریکی به نقطه ای که حداقل سه سیم به یکدگیر میرسند را گره می نامند.
اگر قرار داد کنیم که جریانی که به یک گره وارد می شود را با علامت مثبت و جریانی که از یک گره خارج می شود را با علامت منفی مشخص کنیم ، در این صورت میتوانیم قانون KCL را به صورت زیر بنویسیم :

در واقع این فرمول به ما می گوید که مجموع جریان های الکتریکی ، در هر یک از گره های یک مدار الکتریکی صفر است. قانون جریان کیرشهف بر مبنای پایداری بارهای الکتریکی است و میتوان آن را به این گونه تعبیر کرد که مجموع جریان های وارد شده به یک گره از مدار برابر با مجموع جریان های خارج شده از آن گره می باشد.
اجازه دهید برای درک بهتر این مفهوم مثالی را مطرح کنیم.
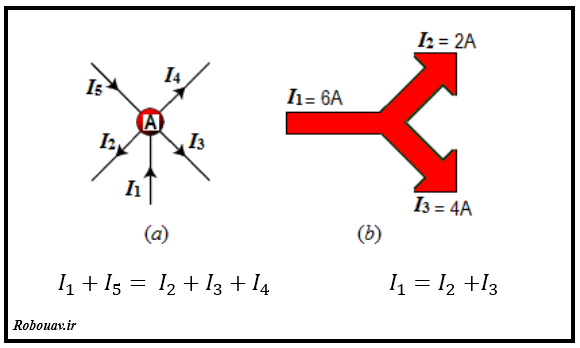
مثال : در گره های زیر به سادگی هر چه تمامی میتوانیم قانون KCL را اعمال کنیم. در این صورت خواهیم داشت :
اجازه دهید برای درک بهتر این قانون مثالی از یک شیر آب مطرح کنیم.
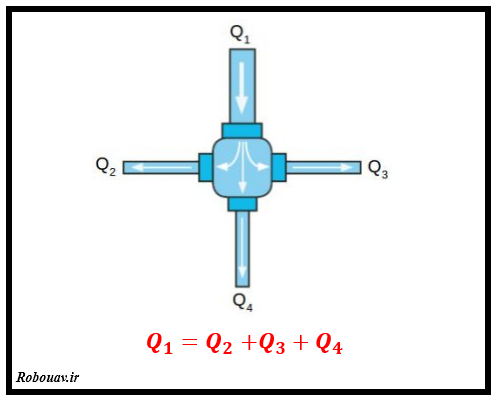
فرض کنید که یک شیرآب داریم که آبی با نرخ Q1 به آن وارد می شود و سه انشعاب شده است و سه نفر دیگر از این آب استفاده میکنند. نرخ استفاده سه نفر دیگر به ترتیب Q2 و Q3 و Q4 می باشد. بدیهی که میتوان رابطه ای شبیه به قانون KCL برای این دستگاه نوشت :
پس قانون کیرشهف چیزی جز پایداری جریان ها نیست. در واقع چون تعداد بارهای الکتریکی قبل از یک گره با تعداد بارهای الکتریکی بعد از آن گره یکی است، میتوانیم از این قانون استفاده کنیم.
حال به معرفی قانون KVL می پردازیم.
قانون KVL
در هر مسیر بسته مجموع ولتاژ باتری ها (emf) ها برابر با مجموع ولتاژ دو سر قطعات است. این قانون با نام قانون ولتاژ و یا قانون مش نیز شناخته می شود. اگر بخواهیم یک رابطه ی ریاضی برای این قانون بنویسیم در این صورت خواهیم داشت:

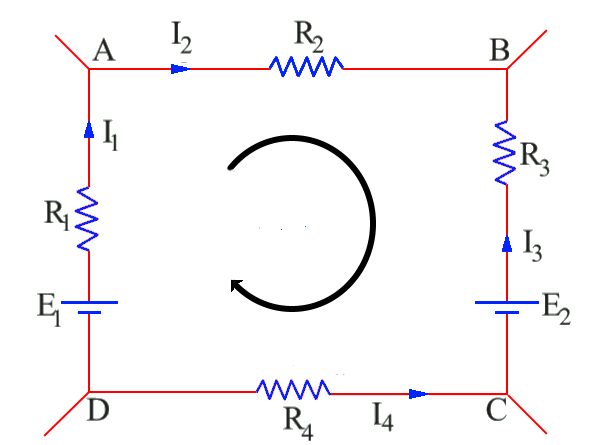
مثال : در شکل زیر یک مدار را مشاهده میکنیم که از دو باتری با ولتاژ های E1 و E2 تشکیل شده است. مجموع ولتاژ کلی باتری ها برابر با E1-E2 است. جریانی تولیدی E1 در جهت عقربه های ساعت است وفرض میکنیم که جهت عقربه های ساعت مثبت باشد. به همین دلیل علامت آن را مثبت در نظر میگریم. علاوه بر آن E2 نیز جریانی در خلافه جهت عقربه های ساعت تولید می کند و فرض میکنیم که این جهت ، جهت منفی باشد. (چون جهت آنها در خلاف جهت یکدیگر است. ). بنابراین هر چیزی که در جهت عقربه های ساعت باشد را مثبت و هر چیزی که در خلاف جهت عقربه های ساعت باشد را منفی در نظر میگیریم.
در شکل زیر جهت های جریان ها مشخص شده است. توجه کنید که همه این ها صرفا یک فرض است و اصلا خودتان را گیج نکنید که این جهت ها از کجا آمده اند. میدانیم که جهت ها در این مدار یا ساعتگرد هستند و یا پادساعتگرد ولی میخواتسیم هر دو جهت را در نظر بگیریم تا با علامت های مثبت و منفی ولتاژ دو سر قطعات آشنا شویم. شما نیز همین فرض را انجام دهید.
حال اگر بخواهیم قانون KVL را برای این مدار بنویسیم در این صورت خواهیم داشت :
![]()
که همانطور که مشاهده میکنید در سمت چپ معادله مجموع انرژی باتری هاست که برابر با E1-E2 می باشد و سمت راست نیز مجموع ولتاژ دو سر قطعات است که چون این قطعات مقاومت هستند ، ولتاژ دو سر آنها برابر با ضرب مقاومت در جریان است. جریان های I1 و I2 را به عنوان جریان مثبت در نظر گرفتیم و به همین خاطر ولتاژ دو سر قطعات مربوط به این جریان ها با علامت مثبت نشان داده شده است. از طرفی دیگر جریان های I3 و I4 را که نیز به عنوان جریان های مفنی در نظر گرفتیم نیز ولتاژ دو سر قطعات آنها با علامت منفی نشان داده شده است.
شاید تا اینجا هنوز مساله برای شما کمی گیچ کننده باشد. به خصوص در بحث علامت جریان ها. به همین خاطر سعی میکنیم با ذکر یک مثال این موضوع را بهتر روشن کنیم.
مثال : در مدار شکل زیر مقدار مقاومت های R1 و R2 و R3 به ترتیب 10 و 4 و 8 اهم می باشد. این مقاومت ها به دو باتری متصل شده اند. مقدار جریان عبوری از هر مقاومت را بیابید.
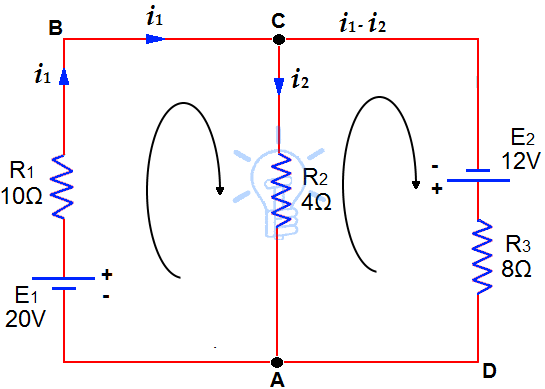
اولین فرضی که انجام می دهیم در مورد جهت حلقه هاست. فرض میکنیم جهت عقربه های ساعت به عنوان جهت مثبت است و این جهت را به عنوان جهت حلقه ها در نظر میگیریم.
فرض کنید جهت جریان همان جهت های نشان داده شده در شکل می باشد. علاوه بر آن فرض میکنیم جریان در خط ABC برابر i1 باشد. همچنین جریان در خط CA را برابر i2 در نظر میگیریم. با توجه به قانون KCL می دانیم که جریان در سیم CDA نیز برابر با i1-i2 می باشد.
حال قانون KVL را در مش ABC اعمال میکنیم. جریان تولیدی E1 در حهت معیار می باشد. به همین خاطر علامت آن را مثبت در نظر میگیریم. بنابراین یک مثبت 20 را در سمت راست معادله خود مینویسیم و در سمت چپ نیز باید با توجه به جهت حلقه ، ولتاژ های دو سر قطعات را محاسبه کنیم. پس :
![]()
در بالا چون جهت های i1 و I2 هر دو در جهت معیار ما (جهت عقربه های ساعت) بوده اند ، به همین علت ولتاژ دو سر قطعات آنها نیزبا علامت مثبت مشخص شده اند.
حال بیایید و قانون KVL را برای حلقه 2 بنویسیم. چون جهت جریان تولیدی E2 در جهت معیار می باشد ، پس مقدار آن را در سمت راست به صورت مثبت در نظر میگیریم. جهت جریان i1-i2 نیز در جهت جریان معیار می باشد و بنابراین هر قطعه ای که این جریان از آن عبور می کند ، ولتاژ دو سر آن با علامت مثبت مشخص می شود. ضمن این که جهت جریان i2 در خلاف جهت معیار می باشد. بنابراین باید ولتاژ دو سر آن را با علامت منفی در نظر گرفت. پس میتوانیم معادله KVL برای این حلقه را به صورت زیر بنویسیم :
![]()
حال با دو معادله و دو مجهول روبرو هستیم. با حل این معادله جریان های بدست آورده شده به صورت i1 = 1.895A و i2=0.263 آمپر می باشد. پس i1-i2 نیز برابر با 1.632 آمپر می شود. بنابراین توانستیم به سادگی جریان های عبوری از این مقاومت ها را بدست آوریم.
حال اگر بخواهیم این جهت ها و جهت گیری ها و علامت های آنها را در چند قانون خلاصه کنیم خواهیم داشت :
- ولتاژ دو سر یک قطعه که جهت جریان آن مطابق با جهت معیار در نظر گرفته شده است ، با علامت مثبت نشان داده می شود.
- ولتاژ دو سر یک قطعه که جهت جریان آن خلاف جهت معیار است با علامت منفی نشان داده می شود.
- 3- اگر جهت جریان تولیدی باتری مطابق با جهت معیار باشد ، ولتاژ باتری با علامت مثبت نشان داده می شود و در غیر این صورت ولتاژ باتری را با علامت منفی نشان می دهیم.
در پایان این جلسه برای درک بهتر این جلسه پیشنهاد می شود مثال های زیر را حل کنید:
سوال 1 : در شکل زیر جریان عبوری از مقاومت های 2 اهم و 4 اهم و 8 اهم را بدست آورید. در پایان مثل همیشه میتوانید ما را در تلگرام و یا اینستاگرام دنبال کنید : نقشه راه دوره الکترونیک: 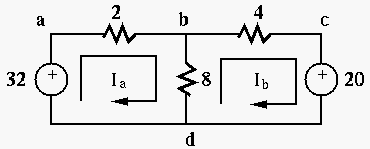





دیدگاهتان را بنویسید