آشنایی با فیلتر پایین گذر به زبان ساده
مقدمه
در این جلسه قصد داریم به معرفی فیلتر پایین گذر بپردازیم. این جلسه یکی از جلسات پیش نیاز مربوط به دوره LTSPICE می باشد که قصد داریم مدار آن را شبیه سازی کنیم. ولی قبل از شبیه سازی ابتدا تیوری مربوط به فیلتر پایین گذر را توضیح دهیم. مثل همیشه بدون اتلاف وقت وارد اصل مطلب می شویم .
فیلتر پایین گذر چیست ؟
بیایید بحث را با یک آهنگ شروع کنیم. هر آهنگی که می شنویم از فرکانس های مختلفی تشکیل شده است و فرکانس های مختلف در کنار هم قرار گرفته اند تا این آهنگ را به بهترین شکل ما بشنویم. در نرم افزارهای مربوط به پخش آهنگ قسمتی به نام equalizer وجود دارد که به کمک این قسمت میتوانیم باندهای فرکانسی مختلف را مشاهده کنیم. مثلا در نرم افزار pot player این بخش به شکل زیر می باشد :
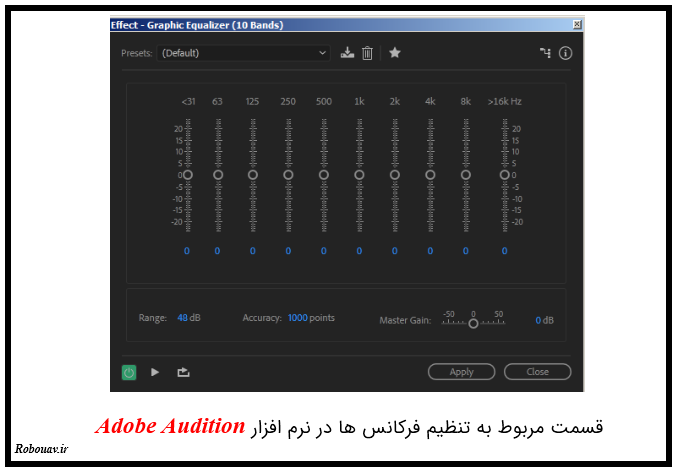
همانطور که میبینید ما چندین خط تنظیم داریم که میتوانیم به کمک این چند خط مشخص کنیم که دوست داریم چه فرکانس هایی در خروجی قرار بگیرد و چه فرکانس هایی نیز قرار نگیرند.
صدای زیر را به عنوان یک صدای نمونه که هیچ فیلتری بر روی آن اعمال نشده است در نظر بگیرید:
حال اگر خطوط تنظیم کننده را به صورت زیر تغییر دهیم :
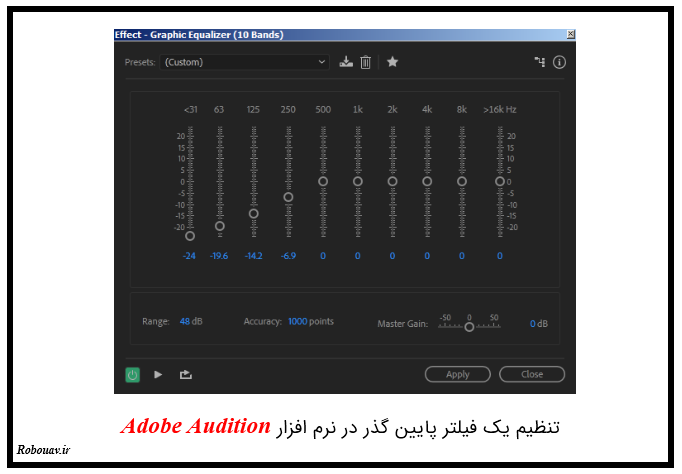
صدا به شکل زیر خواهد بود :
این کار دقیقا مشابه با فیلتر پایین گذر می باشد. در واقع ما به کمک خطوط تنظیم مشخص کرده ایم که فیلترهایی با فرکانس های پایین از خروجی عبور نکنند. همانطور که میبینید با انجام فیلتر پایین گذر فرکانس های پایین تر حذف شده اند و در واقع ما صدای بیس را از دست داده ایم. چون صدای بیس توسط فرکانس های پایین تر تولید می شود.
در صورتی که دوست دارید صداهای مختلف تولیدی توسط فرکانس های متفاوت را بشنوید پیشنهاد می شود از لینک زیر استفاده کنید تا به درک بهتری برسید:
توجه کنید که صداهایی که ما می شنویم باید فرکانس آنها بین 20 هرتز تا 20 کیلوهرتز باشند. حتما اسلایدر مربوط به سایت بالا را حداقل روی 20 قرار دهید. (البته شنیدن فرکانس 20 هم کمی برای ما سخت است و از حدود 30 هرتز شنیدن صدا ملموس تر می باشد. )
همین کار را برای فرکانس های بالا نیز انجام دهید و یک فیلتر بالا گذر بسازید و سعی کنید نتیجه را ببینید. (اگر به adobe audition دسترسی ندارید میتوانید خیلی ساده تر از نرم افزارهای پخش آهنگ و ویدیو مثل pot player استفاده کنید.)
حالا که با مفهوم فیلترپایین گذر آشنا شده ایم بیایید در عمل نیز کمی دقیق تر آن ها را بررسی کنیم.
مدار مربوط به فیلتر پایین گذر
در عمل به کمک یک مقاومت و یک خازن میتوانیم یک فیلتر پایین گذر بسازیم. مدار مربوط به یک فیلتر پایین گذر با خازن و مقاومت به شکل زیر است :
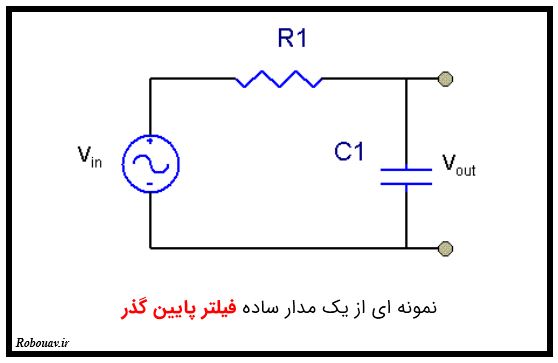
اما سوالی که پیش می آید این است که چگونه این مدار میتواند فرکانس های مختلف را فیلتر کند؟
اول نکته ای که باید به آن توجه کنیم این است که ورودی این مدار یک منبع تغذیه سینوسی است. میدانیم منبع تغذیه سینوسی یک موج سینوسی را در خروجی خود تولید می کند. علاوه بر آن از تبدیل فوریه نیز به یاد داریم که یک موج سینوسی از فرکانس های مختلفی تشکیل شده است تا چنین موجی تولید شود. یعنی فرکانس های مختلف با یکدگیر جمع شده اند و تشکیل این موج را داده اند.
حال ما ادعا میکنیم که این مدار میتواند فرکانس هایی پایینی که تشکیل دهنده موج سینوسی ورودی هستند را فیلتر کند و در خروجی خود فقط فرکانس های بالای این منبع تغذیه را نشان دهد. علت چیست ؟
در جلسه مربوط به کاربرد خازن ها گفتیم که خازن فرکانس های بالا رو عبور میده و در مقابل فرکانس های پایین مقاومت میکنه. (در مورد علت این موضوع در جلسه مربوط به خازن ها توضیح داده شده.). پس کل داستان مربوط به ویژگی خازن است. (البته برای بحث دقیق تر لازم است تا معادلات حاکم بر این مدار نوشته شود و به صورت دقیق صحبت شود ولی به دلیل طولانی نشدن متن از آن صرف نظر میکنیم.)
نمودار خروجی یک فیلتر پایین گذر
قبل از این که خروجی نمودار فیلتر پایین گذر را با یکدیگر بررسی کنیم اجازه دهید چند اصطلاح را با یکدیگر مرور کنیم :
1- پاسخ فرکانسی : پاسخ فرکانسی یک مدار الکتریکی به ما این اجازه را می دهد تا بهره و فاز خروجی را در یک فرکانس مشخص مشاهده کنیم. در واقع با کمک پاسخ فرکانسی میتوانیم بفهمیم که مثلا در فرکانس 70 هرتز نسبت دامنه سیگنال خروجی به دامنه سیگنال ورودی چقدر بوده است. حال اگر این نسبت را برای همه فرکانس ها محاسبه کنیم و یک نمودار رسم کنیم ، به پاسخ فرکانسی بهره (نسبت خروجی به ورودی) می رسیم.
به کمک پاسخ فرکانسی میتوانیم بفهمیم که مدار ما در فرکانس های مختلف چه بلایی بر سر سیگنال ورودی می آورد و میتوانیم رفتار آن مدار را تحلیل کنیم.
واضح است که در یک نمودار پاسخ فرکانسی، محور x ها همان فرکانس های ما می باشند و محور y ها هم همان نسبت خروجی به ورودی می باشند.
2- نمودار Bode : نمودار Bode در واقع همان پاسخ فرکانسی است که در فرکانس های مختلف نسبت ورودی به خروجی محاسبه شده اند و به شکل یک نمودار رسم شده است و ما به کمک آن میتوانیم به تحلیل مدار خود بپردازیم.
3- دسی بل : به 20 (و گاهی اوقات 10) برابر لگاریتم ولتاژ خروجی به ولتاژ ورودی یک دسی بل گفته می شود. در واقع :

واحد محور عمودی در دیاگرام Bode دسی بل می باشد.
حال آماده ایم تا نمودار خروجی یک فیلتر پایین گذر را مشاهده کنیم :
ابتدا شکل زیر را ببینید:
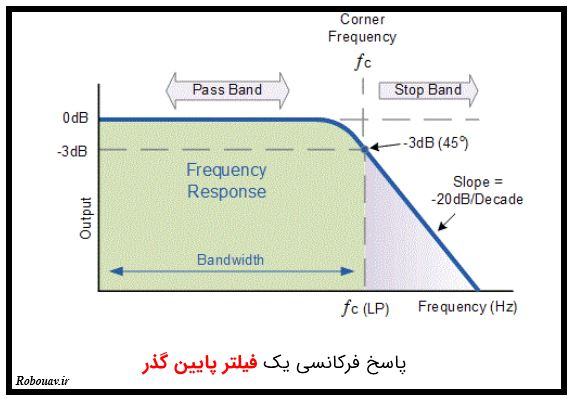
لطفا قبل از خواندن ادامه این مطلب لطفا بار دیگر به این شکل نگاه کنید و تحلیل کنید که چرا نمودار Bode مربوط به یک فیلتر پایین گذر چنین شکلی است.
در فرکانس های پایین که سیگنال ورودی دقیقا به خروجی می رود. پس ورودی برابر با خروجی است و اگر مقدار بهره را بر حسب دسی بل محاسبه کنیم به عدد صفر می رسیم. چون لگاریتم 1 برابر صفر می باشد. به همین خاطر انتظار داریم در فرکانس های پایین مقدار بهره برابر صفر باشد که همین اتقاق نیز رخ داده است.
اما فرکانس که بالاتر می رود کم کم عبور سیگنال ها سخت می شود و ولتاژ خروجی نسبت به ورودی مقدار کمتری دارد. پس نسبت این دو کمتر از 1 می باشد و اگر مقدار دسی بل این نسبت را حساب کنیم به عددی منفی می رسیم . پس در فرکانس های بالا انتظار داریم که کم کم مقدار خروجی به اعداد منفی میل کند که همین اتفاق نیز افتاده است.
در این نمودار یک فرکانس مشخص وجود دارد که فرکانس مهمی است. وقتی که نسبت ولتاژ خروجی به ورودی برابر با 0.707 شود مقدار بهره خروجی بر حسب دسی بل برابر با 3- دسی بل می شود. به این فرکانس Cut off Frequency گفته می شود. البته ممکن است با اسم هایی مثل pass Band نیز برای این مورد مواجه شوید. علاوه بر آن به بازه که مقدار بهره خروجی کمتر از 3- دسی بل باشد stop Band گفته می شود.
در پایان این جلسه پیشنهاد می شود برای درک بهتر حتما تمارین زیر را انجام دهید :
سوال 1 : تحقیق کنید که آیا مداری دیگر وجود دارد که بتوانیم به کمک آن یک فیلتر پایین گذر بسازیم ؟ آن مدار چگونه فرکانس های بالا را فیلتر می کند ؟ سوال 2 : نمودار خروجی مربوط به یک فیلتر بالا گذر به صورت زیر می باشد: این نمودار را تحلیل کنید. مثل همیشه میتوانید ما را در تلگرام و یا اینستاگرام دنبال کنید : 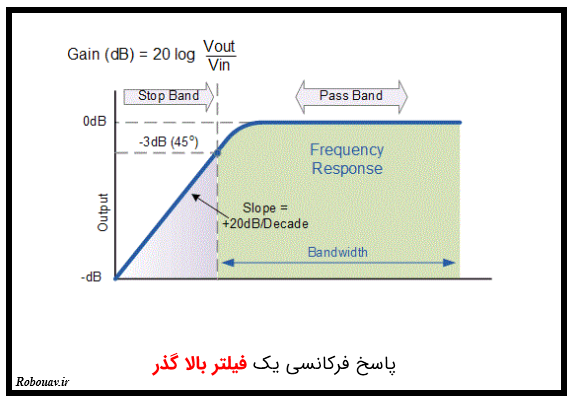





دیدگاهتان را بنویسید