مدارهای سری و موازی- {تفاوت ها،كاربرد و محاسبات آنها در الكترونيك}
[av_one_third first av_uid=’av-64jg0g’]
آنچه در این جلسه خواهیم گفت :
- مفهوم گره
- مفهوم مدارهای سری
- مفهوم مدارهای موازی
- محاسبه مقاومت معادل و حل یک مثال
- خازن های سری و موازی
پیش نیازهای این جلسه :
[/av_one_third] [av_one_third av_uid=’av-86ze8′]میزان پیشرفت در دوره
[skillwrapper type=”gage” align=”left”] [skill percent=”75″ title=”” bar_foreground=”#f00″ bar_background=”#eee”] [/skillwrapper] [/av_one_third]
مفهوم گره
قبل از اينكه وارد بحث سريال و موازي شويم ابتدا لازم است با مفهوم گره (node) آشنايي پيدا كنيم.
تقاطع بين دو يا چند قطعه الكتريكي در مدار را يك گره مي نامند. هنگامي كه يك مدار الكترونيك را شبيه سازي مي كنيد سيم هاي بين دو قطعه يا بيشتر را يك گره مي نامند. شكل زير به طور واضح اين موضوع را نشان مي دهد.
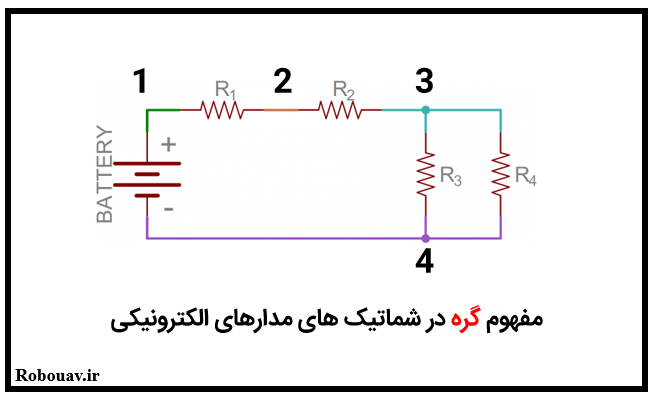
در ادامه نياز داريم بدانيم كه جريان چگونه در مدار جاري مي شود؟ جريان از نقطه با ولتاژ بالاتر به نقطه با ولتاژ پايين تر جريان دارد.
در شكل زير جريان در هر قسمت با رنگ هاي مختلف نشان داده شده است.
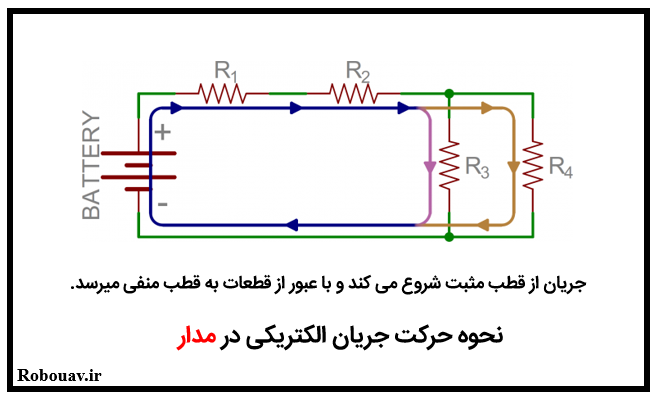
اگر به شكل بالا دقت كنيد متوجه مي شويد كه جريان هنگامي كه از مقاومت هاي R1 و R2 عبور مي كند با همان ميزاني كه وارد مي شود با همان ميزان هم خارج مي شود ولي هنگامي كه بين مقاومت هاي R2 و R3 و R4 عبور مي كند به دو قسمت تقسيم مي شود. اين توضيح تفاوت اساسي بين سري و موازي است.
مدارهای سری
دو قطعه را سري مي نامند هنگامي كه دو شرط زير را داشته باشند:
- داراي گره مشترك باشند
- داراي جريان يكسان باشند.
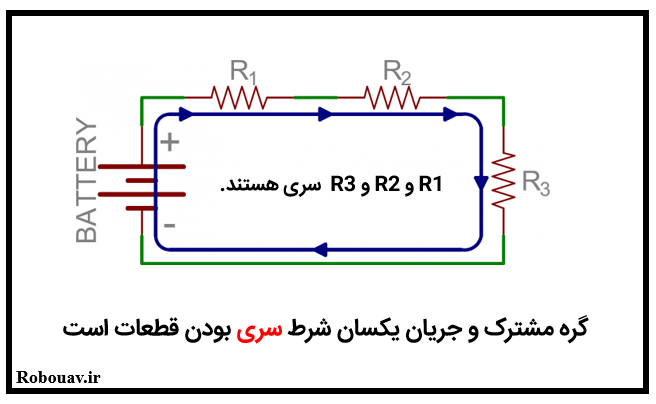
در مدار سري بالا تنها و تنها يك مسير براي عبور جريان است.
مدارهای موازی
دو قطعه را موازي مي نامند هنگامي كه دو شرط زير را داشته باشند:
- داراي دو گره مشترك باشند
- داراي ولتاژ يكسان باشند.
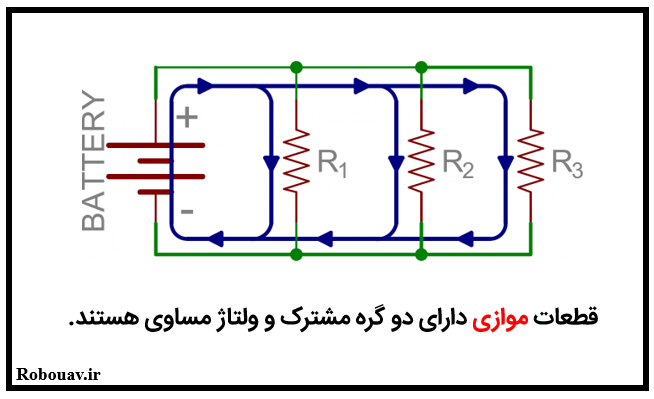
مدارهای سری و موازی
در اينگونه مدارها تعدادي از قطعات با هم سري هستند و تعدادي ديگر با هم موازي هستند.
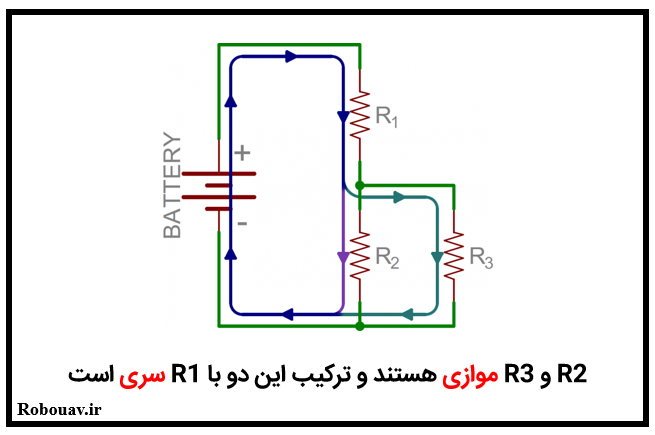
محاسبه مقاومت معادل در مدارهاي سري
براي محاسبه مقاومت معادل ابتدا يك مدار ساده را در نظر مي گيريم و جريان عبوري از مقاومت را محاسبه مي كنيم.
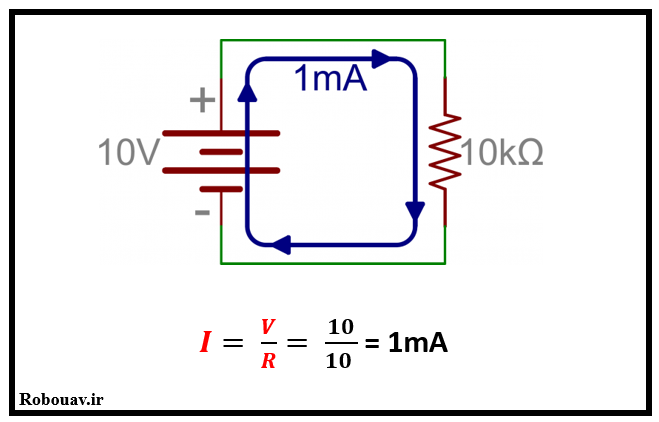
چنانچه يك مقاومت ديگر را با مقاومت فوق سري كنيم به صورت زير است.
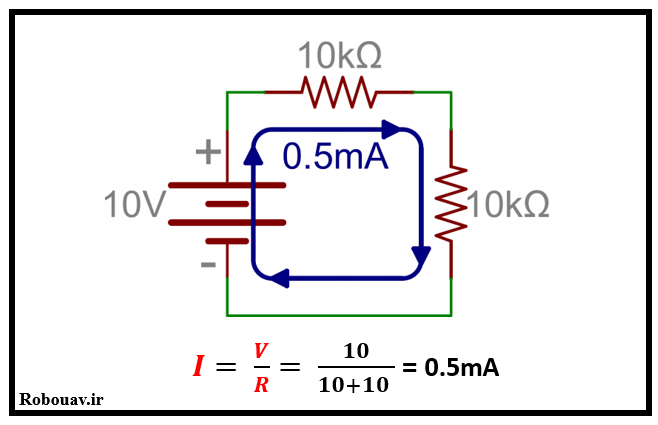
براي تعداد زياد مقاومت به صورت زير عمل مي كنيم.
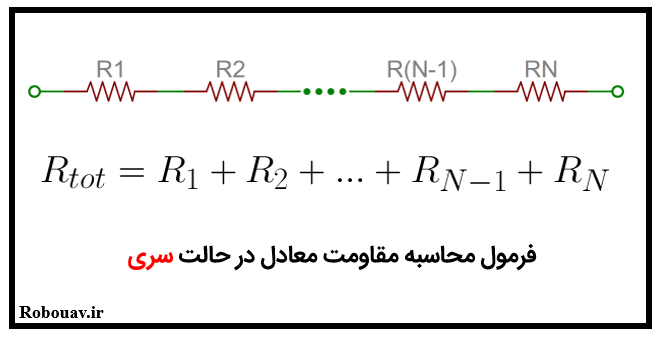
محاسبه مقاومت معادل در مدارهاي موازي
در مدارهاي موازي عكس مقاومت ها را با هم جمع مي كنيم.
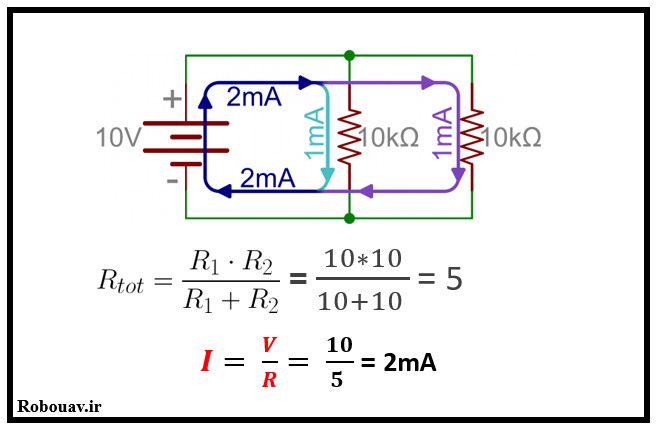
رابطه كلي براي n سري مقاومت به صورت زير است.
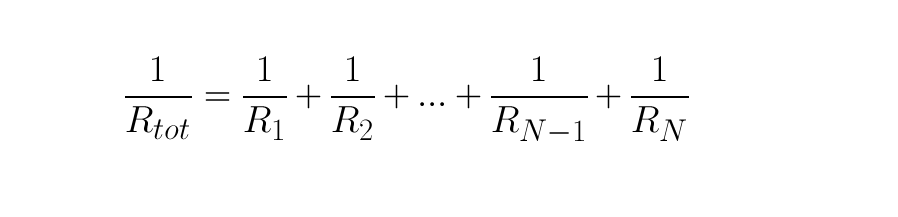
محاسبات خازن هاي سري و موازي
براي خازنها به صورت زير محاسبات را انجام مي دهيم.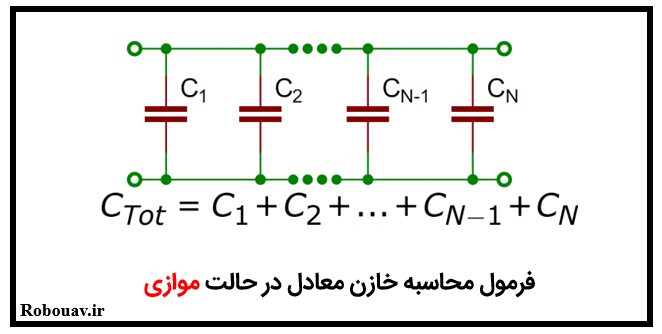
در خازن هاي سري به صورت زير محاسبات را انجام مي دهيم.
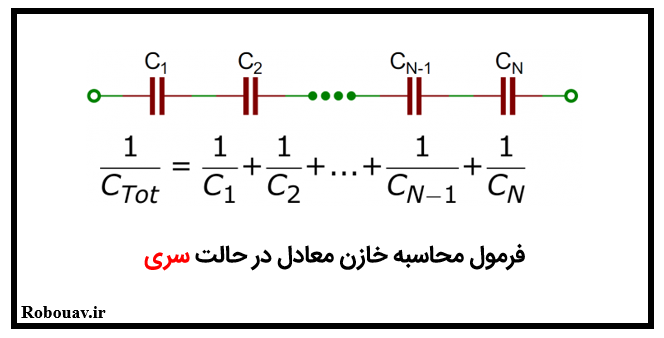
خوب دوستان به پایان این جلسه رسیدیم. پیشنهاد ما این است که جلسه دوم این آموزش با نام “انجام چند آزمایش با مدارهای سری و موازی و مفهوم ثابت زمانی” را از لینک زیر مطالعه کنید تا به این مبحث تسلط کافی پیدا کنید:
مثل همیشه میتوانید ما را در تلگرام و یا اینستاگرام دنبال کنید.
28 دیدگاه
به گفتگوی ما بپیوندید و دیدگاه خود را با ما در میان بگذارید.





سلام جزوه تحلیل مدارهای الکتریکی رو میخواستم مال سری و موازی ب زبان ساده اگه میشه راهنمایی کنید ممنون میشم
با سلام.
متاسفانه اینجا ما جزوه ای ارایه نمی دهیم و محتواهای آموزشی صرفا از طریق همین مطالب ارایه می شوند.
موفق باشید.
با سلام ! اگر ممکن هستش در مورد نحوة عملکرد ترانزيستور و نحوة اتصال پايه هاي آن در مدار همچنين اصول و قاعده کلي در مورد تحليل و ساخت يک مدار را توضيح دهيد يا سپاس
با سلام. در مورد ترانزیستور به تفصیل چندین جلسه آورده شده است و به صورت دقیق مدارات کاربردی آن بررسی شده است. لینک این مطالب در زیر آورده شده است :
جلسه اول – مقدمه و معرفی
جلسه دوم – بررسی ساختار و نحوه کار ترانزیستور
جلسه سوم – بررسی حالت های کاری ترانزیستور
جلسه چهارم – ترانزیستور در نقش یک کلید
جلسه پنجم – ترانزیستور در نقش یک تقویت کننده
علاوه بر آن یک جلسه نیز در مورد ماسفت ها منتشر شده است که از این لینک میتوانید به آن دسترسی داشته باشید.
موفق باشید.
با سلام.اگر در یک مدار مقاومت ها هم به صورت سری و هم موازی باشند مقاومت را چگونه به دست می آوریم؟?
با سلام.
در کامنت قبل پاسخ داده شد.
موفق باشید.
با سلام.اگر در یک مدار مقاومت ها هم به صورت سری و هم موازی باشند مقاومت را چگونه به دست می آوریم؟
با سلام.
در صورت استفاده همزمان از مقاومت های سری و موازی باید از ترکیب روش ها استفاده کنید. یعنی ابتدا مقاومت هایی که ترکیب آنها مشخص است را بیابید. مثل اگر چند مقاومت سری هستند ابتدا مقاومت آنها را حساب کنید و سپس به مدار خود مجددا نگاه کنید و ببینید که آیا ترکیبی مثل سری یا موازی بودن میبینید یا خیر و این کار را تا انتها ادامه دهید.
موفق باشید.